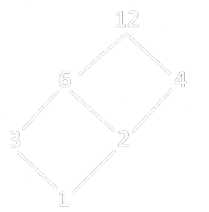
Modulo 9
Reticolo¶
Definizione ― Reticolo
Un Reticolo è un insieme parzialmente ordinato \(S\) tale che, per ogni \(a, b \in S\), esistono \(inf(a,b)\) e \(sup(a,b)\).
\[
\begin{array}{c}
\forall \text{ } a,b \in A \\
\exists \text{ } sup(a,b) \text{ e } inf(a,b)
\end{array}
\]
Definizione ― Estremi
- L'estremo inferiore (detto anche Meet, rappresentato con il simbolo \(\mathop{\wedge}\)) è il più grande di tutti quegli elementi che sono più piccoli di \(a\) e \(b\).
\[
\begin{array}{c}
a \mathop{\wedge} b = inf(a,b)
\end{array}
\]
- L'estremo superiore (detto anche Join, rappresentato con il simbolo \(\mathop{\vee}\)) è il più piccolo di tutti quegli elementi che sono più grandi di \(a\) e \(b\).
\[
\begin{array}{c}
a \mathop{\vee} b = sup(a,b)
\end{array}
\]
Proprietà Algebriche
- Commutatività: l'ordine degli elementi non influenza il risultato.
\[
\begin{array}{c}
x \mathop{\wedge} y = y \mathop{\wedge} x \\
y \mathop{\vee} x = x \mathop{\vee} y
\end{array}
\]
- Associatività: la disposizione delle parentesi non influenza il risultato.
\[
\begin{array}{c}
x \mathop{\wedge} (y \mathop{\wedge} z) = (x \mathop{\wedge} y) \mathop{\wedge} z \\
x \mathop{\vee} (y \mathop{\vee} z) = (y \mathop{\vee} x) \mathop{\vee} z
\end{array}
\]
- Assorbimento: assicura che combinare un elemento con il risultato dell'intersezione (o unione) dell'elemento con un altro non cambia il risultato.
\[
\begin{array}{c}
x \mathop{\wedge} (x \mathop{\wedge} y) = x \\
x \mathop{\vee} (x \mathop{\vee} y) = x
\end{array}
\]
- Idempotenza: l'operazione applicata due volte all'elemento restituisce l'elemento stesso.
\[
\begin{array}{c}
x \mathop{\wedge} x = x \\
x \mathop{\vee} x = x
\end{array}
\]
Esempio
- Traccia: identificare un reticolo dato un insieme ed una relazione.
STEP 1: Analisi dell'Insieme e Relazione di partenza
- \(A = \{1,2,3,4,6,12\}\)
- \(\mathcal{R} = \{(a,b) \in A : a \leq b \text{ se e solo se } a \mid b\}\)
Nozione di Divisibilità
- Un numero \(a\) divide il numero \(b\) se esiste un numero intero \(k\) tale che \(b = a \cdot k\).
STEP 2: Verifica delle Proprietà di Ordinamento Parziale
- Riflessività: ogni elemento è divisibile per sé stesso.
- \(1 \mid 1\)
- \(2 \mid 2\)
- \(\dots\)
- Conclusione: la proprietà Riflessiva è rispettata
.
- Antisimmetria: se \(a \mid b\) e \(b \mid a\), necessariamente \(a = b\).
- (Esempio 1) \(a = 2, b = 4\); \(a \mid b: 4 = 2 \cdot 2\), quindi \(2 \mid 4\).
- (Esempio 1) \(b = 4, a = 2\); \(b \not\mid a: 2 \neq 4 \cdot k\) per nessun \(k \in \mathbb{N}\).
- (Esempio 2) \(a = 12, b=12\); \(a \mid b:12=12 \cdot 1\), quindi \(12 \mid 12\).
- (Esempio 2) \(b = 12, a =12\); \(b \mid a: 12 = 12 \cdot 1\), quindi \(12 \mid 12\).
- \(\dots\)
- Conclusione: la proprietà Antisimmetrica è rispettata
perchè quando viene applicata (\(a \mathcal{R} b\) e \(b \mathcal{R} a\)), allora \(a = b\). In tutti gli altri casi, la proprietà Antisimmetrica non viene violata.
- Transitività: se \(a \mid b\) e \(b \mid c\), allora necessariamente \(a \mid c\).
- \(a = 2, b=4, c=12\)
- \(a \mid b : 4 = 2 \cdot 2\); quindi \(a \mid b\).
- \(b \mid c : 12 = 4 \cdot 3\); quindi \(b \mid c\).
- \(a \mid c : 12 = 2 \cdot 6\); quindi \(a \mid c\).
- \(\dots\)
- Conclusione: la proprietà Transitiva è rispettata
.
STEP 3: Verifica delle Proprietà di un Reticolo
- Idempotenza: l'operazione applicata due volte all'elemento restituisce l'elemento stesso.
\[
\begin{array}{c}
4 \mathop{\vee} 4 = mcm(4,4) = 4 \\
6 \mathop{\wedge} 6 = mcd(6,6) = 6 \\
\dots
\end{array}
\]
- Conclusione: la proprietà Idempotenza è rispettata
.
- Commutatività: l'ordine degli elementi non influenza il risultato.
\[
\begin{array}{c}
2 \mathop{\vee} 6 = mcm(2,6) = 6 \\
6 \mathop{\vee} 2 = mcm(6,2) = 6 \\
4 \mathop{\wedge} 6 = mcd(4,6) = 2 \\
6 \mathop{\wedge} 4 = mcd(6,4) = 2 \\
\dots
\end{array}
\]
- Conclusione: la proprietà Commutativa è rispettata
.
-
Associatività: la disposizione delle parentesi non influenza il risultato.
\[ \begin{array}{c} (2 \mathop{\vee} 3) \mathop{\vee} 4 \\ = mcm(2,3) \mathop{\vee} 4 \\ = 6 \mathop{\vee} 4 \\ = mcm(6,4) = 12 \\ \\ 2 \mathop{\vee} (3 \mathop{\vee} 4) \\ = 2 \mathop{\vee} mcm(3,4) \\ = 2 \mathop{\vee} 12 = 12 \\ --- \\ (2 \mathop{\wedge} 3) \mathop{\wedge} 4 \\ = mcd(2,3) \mathop{\wedge} 4 \\ = 1 \mathop{\wedge} 4 = mcd(1,4) = 1 \\ \\ 2 \mathop{\wedge} (3 \mathop{\wedge} 4) \\ = 2 \mathop{\wedge} mcd(3,4) \\ = 2 \mathop{\wedge} 1 = mcd(2,1) = 1 \\ \\ \dots \end{array} \] -
Conclusione: la proprietà Associativa è rispettata
.
- Assorbimento: assicura che combinare un elemento con il risultato dell'intersezione (o unione) dell'elemento con un altro non cambia il risultato.
\[
\begin{array}{c}
4 \mathop{\vee} (4 \mathop{\wedge} 6) \\
= 4 \mathop{\vee} mcd(4,6) \\
= 4 \mathop{\vee} 2 \\
= mcm (4,2) = 4 \\
\\
6 \mathop{\vee} (6 \mathop{\wedge} 12) \\
= 6 \mathop{\vee} mcd(6,12) \\
= 6 \mathop{\vee} 6 \\
= mcm(6,6) = 6 \\
--- \\
4 \mathop{\wedge} (4 \mathop{\vee} 6) \\
= 4 \mathop{\wedge} mcm(4,6) \\
= 4 \mathop{\wedge} 12 \\
= mcd(4,12) = 4 \\
\\
6 \mathop{\wedge} (6 \mathop{\vee} 12) \\
= 6 \mathop{\wedge} mcm(6,12) \\
= 6 \mathop{\wedge} 12 \\
= mcd(6,12) = 6 \\
\\
\dots
\end{array}
\]
- Conclusione: la proprietà di Assorbimento è rispettata
, quindi possiamo stabilire che l'insieme \(A = \{1,2,3,4,6,12\}\) con la relazione \(\mathcal{R}\) di divisibilità è un Reticolo.