Modulo 8

Cardinalità¶

Definizione ― Cardinalità

La Cardinalità di un insieme $A$ indicata con $|A|$, è la classe di equipotenza (numero di elementi) di $A$.

\[ \begin{array}{c} |A| \leq |B| \text{ se esiste } f \text{ iniettiva } A \rightarrow B \\ \text{invece, se } |A| \leq |B| \text{ e } |B| \leq |A|, \text{ allora } |A| = |B| \end{array} \]

Definizione ― Cardinalità di una Funzione

La Cardinalità dell'insieme delle Funzioni da $A \rightarrow B$ è uguale a $|B|^{|A|}$.

Definizione ― Equipotenza

$A$ si dice equipotente a $B$ se esiste una biiezione $A \rightarrow B$ ed una Relazione di Equivalenza su essi.

Teorema di Cantor¶

Definizione ― Teorema di Cantor

Se esistono $A \rightarrow B$ e $B \rightarrow A$ iniettive, allora esiste $A \rightarrow B$ biiettiva.

Esempio

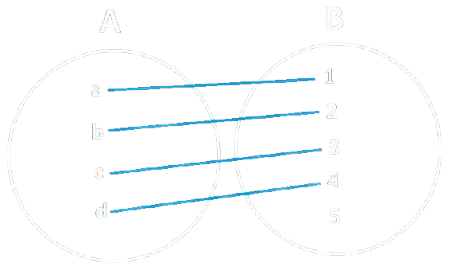
Nell'esempio 1, c'è una funzione iniettiva $A \rightarrow B$, ma non c'è una l'iniettività $B \rightarrow A$, quindi la cardinalità di $A$ è minore di quella di $B$:

\[ \begin{array}{c} |A| < |B| \end{array} \]

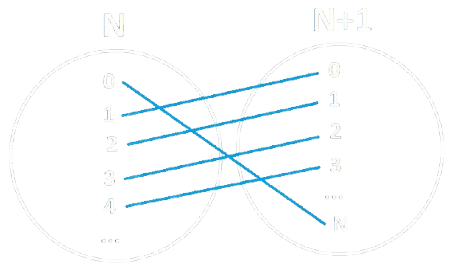
Nell'esempio 2, c'è una funziona iniettiva $A \rightarrow B$ ed una funzione iniettiva $B \rightarrow A$, quindi secondo il Teorema di Cantor, esiste una funzione biiettiva $A \rightarrow B$:

\[ \begin{array}{c} |\mathbb{N}| = |\mathbb{N}+1| \end{array} \]

Alberghi Transfiniti¶

Il matematico Hilbert ha immaginato un albergo con infinite stanze per mostrare alcune caratteristiche dell'infinito stesso.

Caso semplice: arriva un singolo nuovo ospite.

Tutti i clienti già presenti si sposteranno nella camera successiva.
In questo modo, nonostante l'albergo fosse pieno, è possibile far accomodare il nuovo ospite.

Possiamo quindi dedurre che l'albergo può accomodare infiniti clienti più uno:

\[ \begin{array}{c} |\mathbb{N}| = |\mathbb{N}+1| \end{array} \]

Nel caso più complesso: arrivano infiniti nuovi ospiti.

Tutti i clienti si spostano nella stanza $2^n$ (quindi l'ospite 2 si sposta nella camera 4 e così via).
Tutti i nuovi ospiti potranno quindi posizionarsi nelle camere di numero dispari.

\[ \begin{array}{c} |\mathbb{N}| = |\mathbb{N}+\mathbb{N}| \end{array} \]

Nel caso ancora più complesso: ci sono infiniti alberghi con infinite stanze tutte al completo. Tutti gli alberghi chiudono, tranne uno. Tutti gli ospiti vogliono alloggiare nell'unico albergo rimasto aperto.

Ad ogni cliente, viene assegnata una coppia ordinata di numeri $(n,m)$ in cui $n$ rappresenta l'abergo di provenienza e $m$ la relativa stanza.
Successivamente, ad ogni coppia viene assegnata la nuova stanza: $(1,1) \rightarrow 1; (2,1) \rightarrow 2; (1,2) \rightarrow 3; (3,1) \rightarrow 4; \dots$

Possiamo quindi dedurre che ogni insieme infinito avrà sempre la stessa cardinalità?

Supponiamo che:

\[ \begin{array}{c} |\mathbb{N}| = |2^\mathbb{N}| \end{array} \]

Quindi cerchiamo di creare una relazione biiettiva tra l'insieme dei numeri naturali e l'insieme di tutte le sue possibili combinazioni (insieme potenza) e dimostriamo che sono equipotenti.

Mettiamo in forma tabellare la relazione:

-	0	1	2	3	4	...
0	1	0	1	0	1	...
1	1	0	1	1	0	...
2	0	1	1	0	0	...
3	1	1	1	1	1	...
...	...	...	...	...	...	...

Le righe rappresentano l'insieme dei numeri naturali $\mathbb{N}$ mentre le colonne l'insieme di tutti i sottoinsiemi di $\mathbb{N}$.

Ad esempio:

Associamo allo $0$ dell'insieme $\mathbb{N}$ il sottoinsieme di tutti i numeri pari.
Associamo all'$1$ il sottoinsieme $\{0,2,3\}$
Associamo al $2$ il sottoinsieme $\{1,1\}$
Associamo al $3$ l'insieme $\mathbb{N}$ stesso
continuiamo all'infinito $\dots$

Se prendessimo la diagonale dei numeri (nell'esempio raffigurato sono i numeri in grassetto e corsivo):

-	0	1	2	3	4	...
0	1	0	1	0	1	...
1	1	0	1	1	0	...
2	0	1	1	0	0	...
3	1	1	1	1	1	...
...	...	...	...	...	...	...

.. si formerà sicuramente un sottoinsieme presente in $2^\mathbb{N}$, che quindi sarà associato ad un numero naturale dell'insieme $\mathbb{N}$.

Dovremmo quindi trovare su una delle righe una combinazione che corrisponderà all'esatto opposto della diagonale.

Ciò non è possibile perchè nel punto in cui la diagonale ed il complemento si incontreranno, è impossibile che si trovi sia il numero della diagonale che il numero del complemento.

Si è dimostrato quindi che non esiste una funzione suriettiva $\mathbb{N} \rightarrow 2^\mathbb{N}$, e che quindi: $$ \begin{array}{c} |\mathbb{N}| < |2^\mathbb{N}| \end{array} $$

Polvere di Cantor¶

Definizione ― Equipotenza

La polvere di Cantor è un insieme costruito partendo dall'intervallo $[0,1]$ (in una dimensione) e applicando un procedimento iterativo di "rimozione". Alla fine di questo processo, otteniamo un insieme che ha proprietà molto particolari, come essere infinito ma non numerabile e avere misura nulla.

Dimostrazione della Polvere di Cantor

Partiamo dall'intervallo $[0,1]$ sulla retta reale. Questo è l'intervallo di partenza.
- Dividiamo $[0,1]$ in tre parti uguali: $[0,\frac{1}{3}],(\frac{1}{3},\frac{2}{3}),[\frac{2}{3},1]$.
- Rimuoviamo la parte centrale aperta: il segmento $(\frac{1}{3},\frac{2}{3})$.
- Dopo questo primo passo, rimangono due intervalli chiusi: $[0,\frac{1}{3}]$ e $[\frac{2}{3},1]$.
Adesso applichiamo lo stesso procedimento ai due intervalli rimanenti $[0,\frac{1}{3}]$ e $[\frac{2}{3},1]$:
- Dividiamo ciascun intervallo in tre parti uguali: $$ \begin{array}{c} [0,\frac{1}{9}],(\frac{1}{9},\frac{2}{9}),[\frac{2}{9},\frac{1}{3}] \ [\frac{2}{3},\frac{7}{9}],(\frac{7}{9},\frac{8}{9}),[\frac{8}{9},1] \end{array} $$
Rimuoviamo i segmenti centrali aperti di ciascun intervallo:
- Dal primo intervallo $[0,\frac{1}{3}]$, rimuoviamo $(\frac{1}{9},\frac{2}{9})$.
- Dal secondo intervallo $[\frac{2}{3},1]$, rimuoviamo $(\frac{7}{9},\frac{8}{9})$.
Dopo quest'ultimo passo, rimangono 4 intervalli chiusi: $$ \begin{array}{c} [0,\frac{1}{9}],[\frac{2}{9},\frac{1}{3}],[\frac{2}{3},\frac{7}{9}],[\frac{8}{9},1] \end{array} $$
A questo punto, ripetiamo lo stesso procedimento in modo infinito per tutti gli intervalli rimanenti:
- Ad ogni passo, dividiamo ogni intervallo rimanente in tre parti uguali.
- Rimuoviamo sempre il segmento centrale aperto di ciascun intervallo.
Ad esempio, dopo il quarto passo, rimangono 8 intervalli chiusi (uno per ogni estremità dei quattro intervalli del passo precedente). Dopo il quarto passo, ci saranno 16 intervalli, e così via.
Ad ogni iterazione, il numero di intervalli rimanenti raddoppia, ma la loro lunghezza totale diminuisce progressivamente.
Dopo infinite iterazioni, la lunghezza totale rimanente tende a $0$ (poiché $(\frac{2}{3})^n \rightarrow 0$ quando $n \rightarrow \infty$). Quindi, la polvere di Cantor ha misura nulla. Anche se rimangono infiniti punti, la somma della loro lunghezza è $0$.