Modulo 5

Funzione¶

Definizione ― Funzioni

Una Funzione da un insieme $A$ ad un insieme $B$ è una Relazione $\mathcal{R} \subseteq A \times B$ tale che per ogni elemento $a \in A$ esiste uno ed un solo elemento $b \in B$ tale che $a \mathcal{R} b$.

\[ \begin{array}{c} f: A \rightarrow B \end{array} \]

Definizione ― Dominio

Il dominio di una funzione $f$ è l'insieme di tutti i valori (elementi) per i quali la funzione è definita. In altre parole, il dominio è l'insieme di partenza, ovvero l'insieme degli input sui quali la funzione opera.

Definizione ― Codominio

Il codominio di una funzione $f$ è l'insieme di tutti i possibili valori che la funzione può assumere come output. È l'insieme in cui devono appartenere i valori di uscita della funzione.

Definizione ― Immagine

Sia $f : A \rightarrow B$ una funzione che mappa ogni elemento di $A$ (il dominio) in un elemento di $B$ (il codominio). L'immagine di $f$, è l'insieme di tutti i valori che $f(x)$ può assumere quando $x$ varia in $A$. In altre parole, l'immagine è l'insieme dei valori di uscita (output) effettivamente raggiunti dalla funzione.

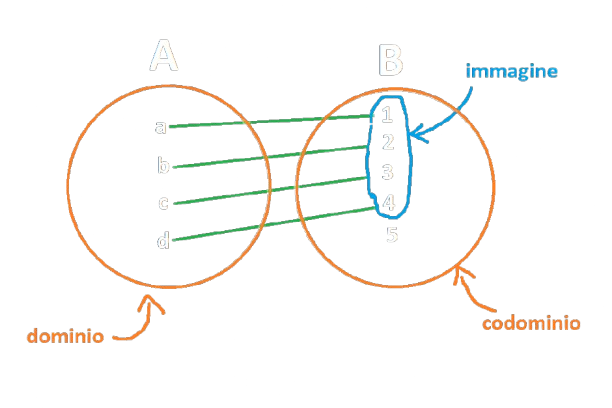
Esempio

Consideriamo la funzione $f: \mathbb{R} \rightarrow \mathbb{R}$ definita come $f(x) = x + 2$.
La funzione $f$ associa ad ogni numero reale $x$ il numero $x + 2$: $$ \begin{array}{c} f(x) = x + 2 \end{array} $$
Il dominio di questa funzione $f$ è l'insieme di tutti i numeri reali $\mathbb{R}$, perchè la funzione è definita per ogni valore di $x \in \mathbb{R}$.
Il codominio di questa funzione è anch'esso $\mathbb{R}$, perchè ogni valore che otteniamo come output dalla funzione è un numero reale. La funzione $f(x) = x + 2$ mappa ogni $x \in \mathbb{R}$ in un altro numero reale.
L'immagine di $f$ è l'insieme di tutti i valori che $f(x)$ può assumere. Poiché la funzione è una traslazione della retta dei numeri reali, l'immagine sarà anch'essa l'insieme di tutti i numeri reali.

Funzioni Iniettive¶

Definizione ― Funzione Iniettiva

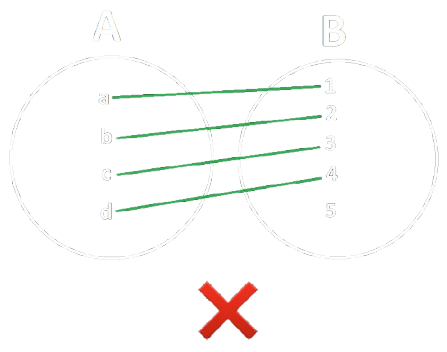
Una funzione si dice iniettiva se per ogni $a$ e $a^\prime$ in $A, f(a) = f(a^\prime)$ implica $a = a^\prime$.

In altre parole, ogni elemento del dominio deve corrispondere ad un solo elemento distinto del codominio.

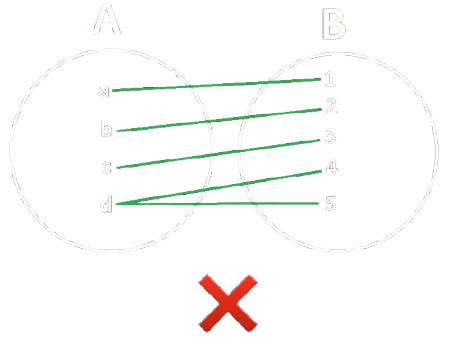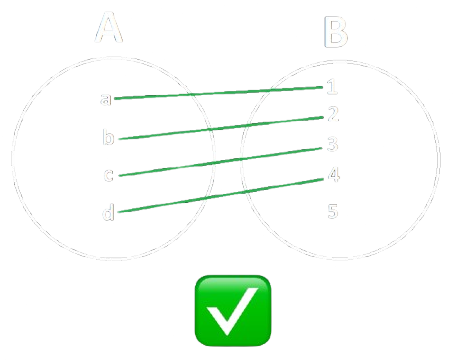Esempio

\[ \begin{array}{c} f(1) = α \\ f(2) = α \\ f(1) \neq f(2) \rightarrow \text{ viola l'iniettività} \end{array} \]

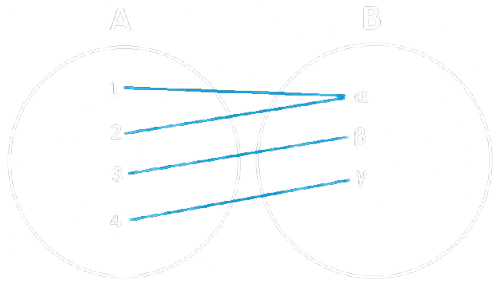
Funzioni Suriettive¶

Definizione ― Funzione Suriettiva

Una funzione si dice suriettiva se per ogni $b$ in $B$ esiste un $a$ in $A$ tale che $f(a) = b$.

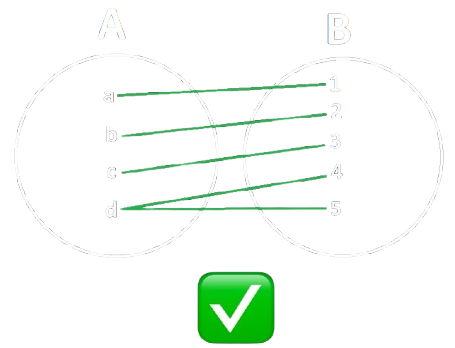Funzioni Biiettive¶

Definizione ― Funzione Biiettiva

Una funzione si dice biiettiva quando è sia suriettiva che iniettiva (detta relazione one-to-one).

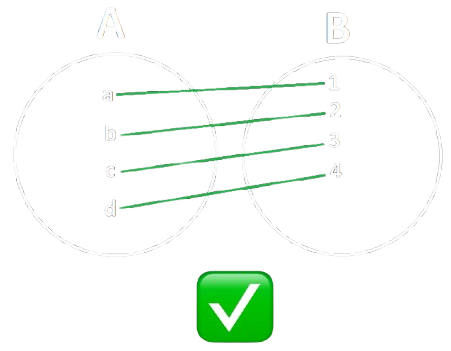
Note aggiuntive

Una Funzione $f : A \rightarrow B$ è biiettiva se e solo se invertendo l'ordine delle coppie si ottiene ancora una funzione (Funzione Inversa).

Infinito e Finito¶

Definizione ― Infinito

Un insieme è detto infinito se è in corrispondenza biunivoca con una sua parte propria (con un suo sottoinsieme proprio).

Definizione ― Numeri Transfiniti

Sono definiti Numeri Transfiniti quei numeri che vanno oltre l'infinito.

Esempio

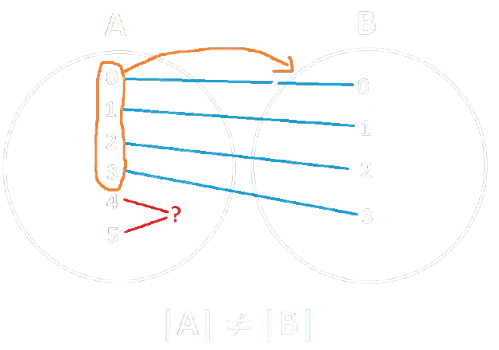
In questo primo esempio:

Sia $A = \{0,1,2,3,4,5\}$ e $B$ un suo sottoinsieme dei primi quattro elementi: $B = \{0,1,2,3\}$.
Associando ogni elemento $a$ di $A$ con un elemento $b$ di $B$ ($f(0) = 0, f(1) = 1$, etc.) rimangono fuori i due elementi $\{4,5\}$.
Questa Relazione non è una funzione biiettiva (non è nemmeno una funzione) quindi possiamo definire $A$ come insieme finito.

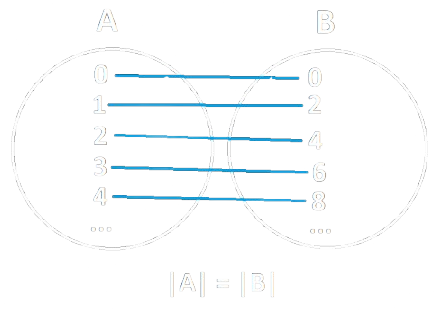
Nel secondo esempio:

Sia $A$ l'insieme dei numeri naturali e $B$ un suo sottoinsieme che contiene tutti i numeri pari.
Associando ogni elemento $a$ di $A$ con il suo doppio $b$ di $B$ ($f(1) = 2, f(2) = 4$, etc.) non rimangono fuori elementi.
La Relazione è quindi una funzione biiettiva perchè rispetta le due proprietà: suriettività e iniettività.
Dato che l'insieme dei numeri naturali è equipotente al suo sottoinsieme che contiene solo i numeri pari, possiamo quindi definire $A$ un insieme infinito.

Funzione Inversa¶

Definizione ― Funzione Inversa

Invertendo l'ordine delle coppie di una funzione non iniettiva o non suriettiva si ottiene una relazione che non è una funzione. Una Funzione per avere la sua inversa deve essere biiettiva.

\[ \begin{array}{c} f^{-1} : B \rightarrow A \end{array} \]

Esempio

Esempio con una Funzione Iniettiva

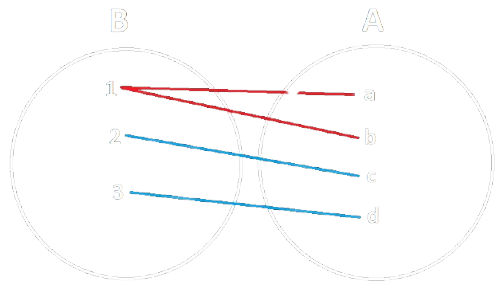
Esempio con una Funzione Suriettiva

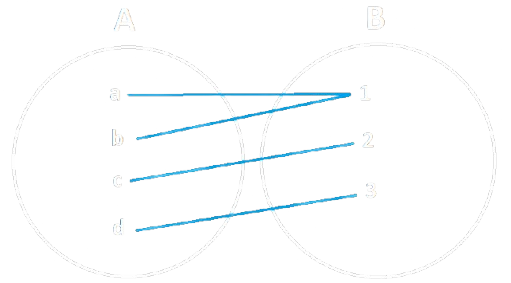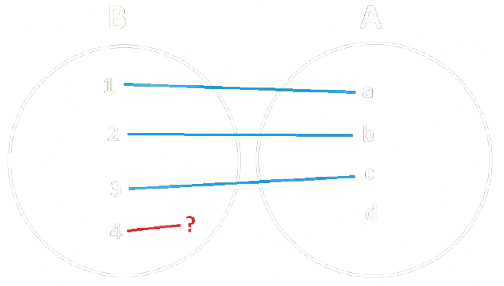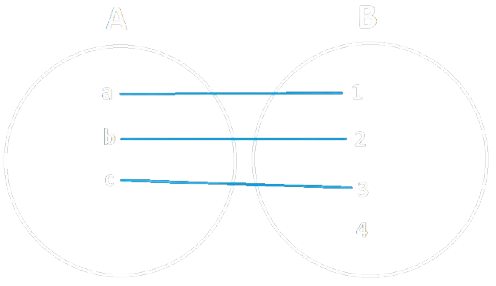
Identità di una Funzione¶

Definizione ― Funzione Indentica

Una Funzione di Identità associa ogni elemento di $A$ a sé stesso.

\[ \begin{array}{c} id_A(a) = a \end{array} \]

Esempio

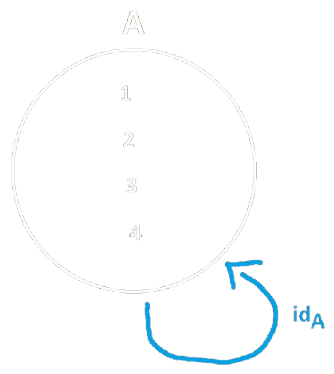
Nell'esempio raffigurato:

\[ \begin{array}{c} id_A(1) = 1 \\ id_A(2) = 2 \\ id_A(3) = 3 \\ id_A(4) = 4 \end{array} \]