Modulo 3

Relazione¶

Definizione ― Relazione

Una Relazione fra due insiemi $A$ e $B$ è un qualunque sottoinsieme di $A \times B$. $$ \begin{array}{c} \mathcal{R} \subseteq A \times B \end{array} $$

Esempio

\[ \begin{array}{c} A = \{1, 2, 3\} \\ B = \{4, 5, 6\} \\ A \times B = \{(1,4),(1,5),(1,6),(2,4),(2,5),(3,6)\} \\ \mathcal{R}_1 = \{(1,6), (2,5)\} \end{array} \]

Composizione di due Relazioni¶

Definizione ― Composizione di due Relazioni

La Composizione di due Relazioni $\mathcal{R}$ ed $\mathcal{S}$ tra gli insiemi $A,B$ e $C$ è definita come una Relazione $\mathcal{R} \circ \mathcal{S} \subseteq A \times C$, tale che per ogni coppia $(a,c) \in \mathcal{R} \circ \mathcal{S}$, esiste un elemento $b \in B$ tale che $a \mathcal{R} b, b \mathcal{S} c$.

Esempio

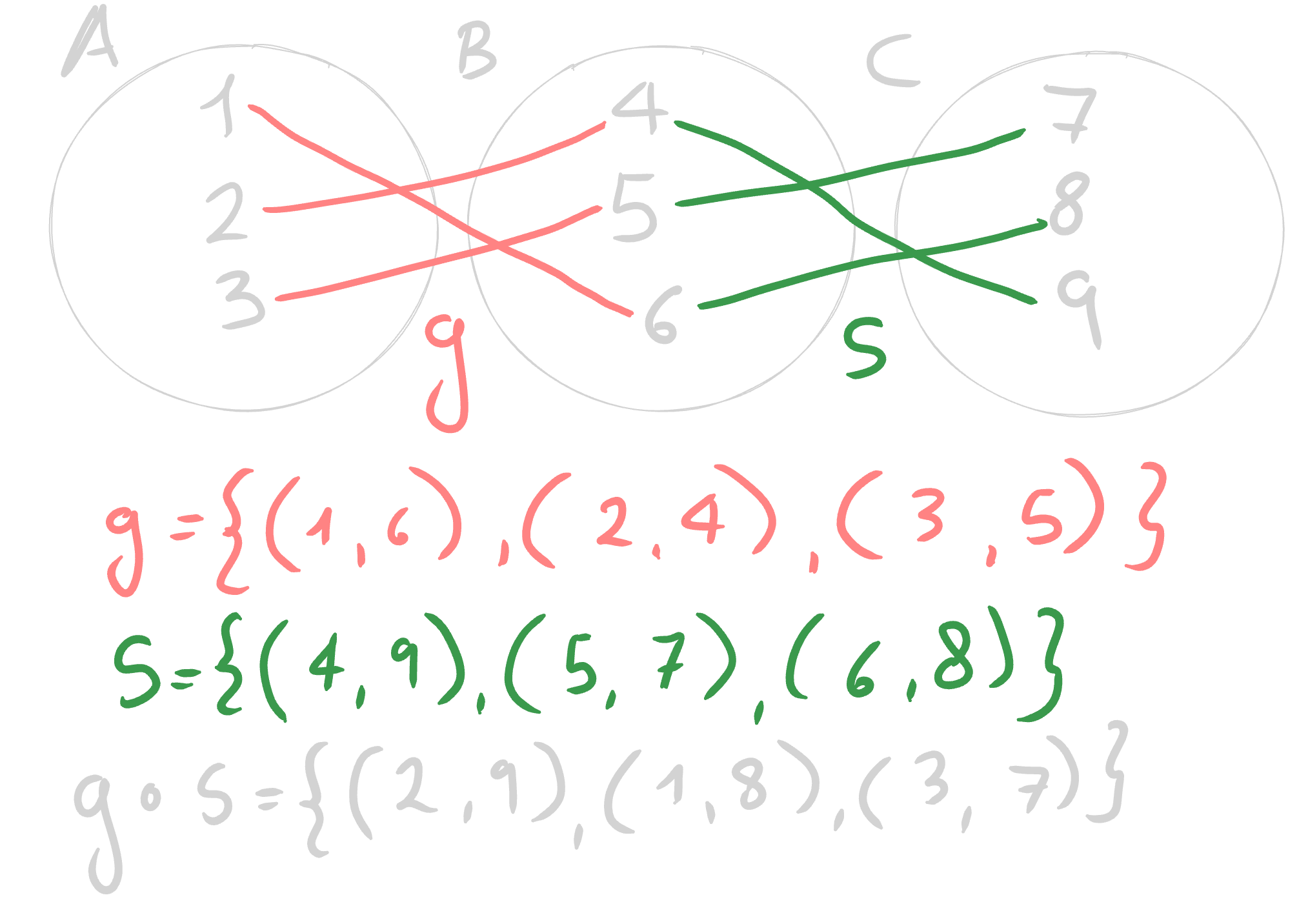
Complemento di una Relazione¶

Definizione ― Complemento di una Relazione

Sia $\mathcal{R}$ una Relazione definita su un insieme $A$. Il complemento di $\mathcal{R}$, denotato $\mathcal{R}^C$, è definito come l'insieme delle coppie ordinate $(a,b)$ in $A \times A$ tali che $(a,b) \not\in \mathcal{R}$.

\[ \begin{array}{c} \mathcal{R}^C = \{(a,b) \in A \times A \, | \, (a,b) \not\in \mathcal{R}\} \end{array} \]

Relazioni Riflessive e Antiriflessive¶

Definizione ― Relazione Riflessiva

\[ \begin{array}{c} \forall a \in A \\ (a,a) \in \mathcal{R} \end{array} \]

Definizione ― Relazione Antiriflessiva

\[ \begin{array}{c} \forall a \in A \\ (a,a) \not\in \mathcal{R} \end{array} \]

Esempio

$\mathcal{R}_1 = \{(a, a) \mid a \in A\}$
- Proprietà: Riflessiva, perché ogni elemento è in relazione con sé stesso.
$\mathcal{R}_2 = \emptyset$
- Proprietà: Antiriflessiva, perché non contiene nessuna coppia $(a, a)$.
$\mathcal{R}_3 = \{(a, b) \mid a, b \in A \text{ e } a \text{ è divisibile per } 2\}$ con $A = \{1, 2, 3, 4\}$
- Proprietà: Non è riflessiva perché gli elementi $1$ e $3$ non sono in relazione con sé stessi. Non è antiriflessiva perché gli elementi $2$ e $4$ sono in relazione con sé stessi.
$\mathcal{R}_4 = \{(a, b) \mid a \text{ divide } b\}$
- Proprietà: Riflessiva, perché ogni numero divide sé stesso.
$\mathcal{R}_5 = \{(a, b) \mid a > b\}$
- Proprietà: Antiriflessiva, perché non esistono $a \in A$ tali che $a > a$.
$\mathcal{R}_6 = \{(a, b) \mid a \leq b\}$
- Proprietà: Riflessiva, perché $a \leq a$ per ogni $a \in A$.
$\mathcal{R}_7 = \{(a, b) \mid a \neq b\}$
- Proprietà: Antiriflessiva, perché nessun elemento è diverso da sé stesso.
$\mathcal{R}_8 = \{(a, b) \mid a \text{ e } b \text{ sono fratelli, con } a \neq b\}$
- Proprietà: Antiriflessiva, perché nessuno è fratello di sé stesso (non esistono coppie $(a, a)$ nella relazione).
$\mathcal{R}_{9} = \{(a, b) \mid a \text{ è antenato di } b\}$
- Proprietà: Antiriflessiva, perché nessuno è antenato di sé stesso.
$\mathcal{R}_{10} = \{(a, b) \mid a \text{ è divisore di } b\}$ su $A = \{1, 2, 3, 4, 6\}$
- Proprietà: Riflessiva, perché ogni numero è divisibile per sé stesso.

Relazioni Simmetriche e Antisimmetriche¶

Definizione ― Relazione Simmetrica

\[ \begin{array}{c} \forall \, (a,b) \in A \\ a \mathcal{R} b \rightarrow b \mathcal{R} a \end{array} \]

Definizione ― Relazione Antisimmetrica

\[ \begin{array}{c} \forall \, (a,b) \in A \\ a \mathcal{R} b, b \mathcal{R} a \rightarrow a = b \end{array} \]

Esempio

$\mathcal{R}_{1} = \{(a, b) \mid a = b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Sia simmetrica che antisimmetrica, perché ogni elemento è in relazione solo con sé stesso.
$\mathcal{R}_{2} = \emptyset$ su $A = \{1, 2, 3\}$
- Proprietà: Sia simmetrica che antisimmetrica, poiché non ci sono coppie che violano nessuna delle due proprietà.
$\mathcal{R}_{3} = A \times A$ su $A = \{1, 2\}$
- Proprietà: Simmetrica, perché se $(a, b) \in \mathcal{R}_3$, allora anche $(b, a) \in \mathcal{R}_3$; non è antisimmetrica, perché $a \neq b$ è possibile.
$\mathcal{R}_{4} = \{(a, b) \mid a \text{ divide } b\}$ su $A = \{1, 2, 4\}$
- Proprietà: Antisimmetrica, perché se $a \mid b$ e $b \mid a$, allora $a = b$.
$\mathcal{R}_{5} = \{(a, b) \mid a \geq b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Antisimmetrica, perché se $a \geq b$ e $b \geq a$, allora $a = b$.
$\mathcal{R}_{6} = \{(a, b) \mid a \text{ e } b \text{ sono fratelli}\}$ su un insieme di persone $P$
- Proprietà: Simmetrica, perché se $a$ è fratello di $b$, allora $b$ è fratello di $a$.
$\mathcal{R}_{7} = \{(a, b) \mid a \neq b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Né simmetrica né antisimmetrica, perché la simmetria è violata dalla proprietà stessa e l'antisimmetria non si applica.
$\mathcal{R}_{8} = \{(a, b) \mid a + b = 0\}$ su $A = \{-2, -1, 0, 1, 2\}$
Proprietà: Simmetrica, perché se $(a, b) \in \mathcal{R}_8$, allora $(b, a) \in \mathcal{R}_8$.
$\mathcal{R}_{9} = \{(a, b) \mid a \leq b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Antisimmetrica, perché se $(a, b) \in \mathcal{R}_9$ e $(b, a) \in \mathcal{R}_9$, allora $a = b$.
$\mathcal{R}_{10} = \{(a, b) \mid a + b \text{ è pari}\}$ su $A = \{1, 2, 3, 4\}$
- Proprietà: Simmetrica, perché se $(a, b) \in \mathcal{R}_{10}$, allora $(b, a) \in \mathcal{R}_{10}$.

Relazioni Transitive & Antitransitive¶

Definizione ― Relazione Transitiva

\[ \begin{array}{c} \forall \, (a,b,c) \in A \\ a \mathcal{R} b, b \mathcal{R} c \rightarrow a \mathcal{R} c \end{array} \]

Definizione ― Relazione Transitiva

\[ \begin{array}{c} \forall \, (a,b,c) \in A \\ a \mathcal{R} b, b \mathcal{R} c \rightarrow a \cancel{\mathcal{R}} c \end{array} \]

Esempio

$\mathcal{R}_{1} = \{(a, b) \mid a = b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Transitiva, perché se $a = b$ e $b = c$, allora $a = c$.
$\mathcal{R}_{2} = \emptyset$ su $A = \{1, 2, 3\}$
- Proprietà: Transitiva, perché non ci sono coppie $(a, b)$, quindi non c'è alcuna violazione della transitività.
$\mathcal{R}_{3} = A \times A$ su $A = \{1, 2\}$
- Proprietà: Transitiva, perché ogni coppia $(a, b)$ è in relazione con ogni altra coppia.
$\mathcal{R}_{4} = \{(a, b) \mid a \leq b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Transitiva, perché se $a \leq b$ e $b \leq c$, allora $a \leq c$.
$\mathcal{R}_{5} = \{(a, b) \mid a > b\}$ su $A = \{1, 2, 3\}$
- Proprietà: Transitiva, perché se $a > b$ e $b > c$, allora $a > c$.
$\mathcal{R}_{6} = \{(a, b) \mid a \text{ è padre di } b\}$ su un insieme di persone $P$
- Proprietà: Antitransitiva, perché se $a$ è padre di $b$ e $b$ è padre di $c$, allora $a$ non può essere padre di $c$.
$\mathcal{R}_{7} = \{(a, b) \mid a \text{ è più vecchio di } b\}$ su $A = \{1, 2, 3, 4\}$
- Proprietà: Transitiva, perché se $a$ è più vecchio di $b$ e $b$ è più vecchio di $c$, allora $a$ è più vecchio di $c$.
$\mathcal{R}_{8} = \{(a, b) \mid a + b \text{ è pari}\}$ su $A = \{1, 2, 3, 4\}$
- Proprietà: Né transitiva né antitransitiva, perché, ad esempio, se $(a, b) \in \mathcal{R}_8$ e $(b, c) \in \mathcal{R}_8$, non è garantito che $(a, c) \in \mathcal{R}_8$.
$\mathcal{R}_{9} = \{(a, b) \mid a + b = 10\}$ su $A = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$
- Proprietà: Né transitiva né antitransitiva, perché non esiste alcuna regola che leghi $a, b, c$ in modo consistente.
$\mathcal{R}_{10} = \{(a, b) \mid a \text{ è divisore di } b\}$ su $A = \{1, 2, 4, 8\}$
- Proprietà: Transitiva, perché se $a \mid b$ e $b \mid c$, allora $a \mid c$.

Chiusura¶

Definizione ― Chiusura

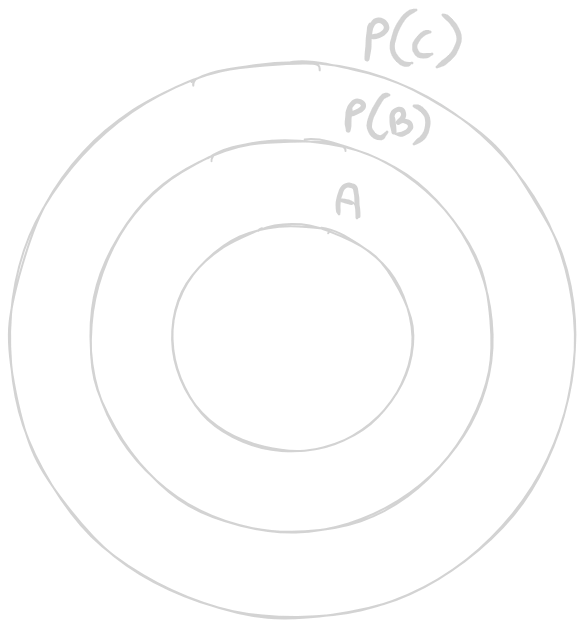
Un insieme $B$ è detto chiusura di un insieme $A$ rispetto ad una proprietà $P$ quando sono soddisfatte le seguenti condizioni:

$B$ gode della proprietà $P$, quindi $P(B)$
$A \subseteq B$
per ogni insieme $C$, se $P(C)$ e $A \subseteq C$, allora $B \subseteq C$

Note aggiuntive

La Chiusura di un insieme rispetto ad una proprietà, se esiste, è unica.

Esempio ― Dimostrazione dell'unicità della Chiusura

Supponiamo di avere $B$ e $B^\prime$ che sono entrambe chiusure di $A$ rispetto a $P$.

Per le tre proprietà della Chiusura, possiamo dire che:

esiste un insieme $P(B^\prime)$
$A \subseteq B^\prime$
$B$ è un superinsieme di $B^\prime$, quindi $B^\prime \subseteq B$.

Ora scambiando i due insiemi ($B$ e $B^\prime$) otteniamo quanto segue:

esiste un insieme $P(B)$
$A \subseteq B$
$B^\prime$ è un superinsieme di $B$, quindi $B \subseteq B^\prime$.

Si nota quindi che $B^\prime \subseteq B$ e $B \subseteq B^\prime$. Possiamo concludere che $B = B^\prime$.

Esempio ― Preservazione della Transitività

Nel paragrafo che segue si va a dimostrare che l'operatore insiemistico di Intersezione preserva la Transitività di due Relazioni.

Supponiamo di avere due relazioni transitive, $\mathcal{R}$ e $\mathcal{S}$.

Se $(a,b),(b,c) \in \mathcal{R} \cap \mathcal{S}$, allora $(a,b),(b,c) \in \mathcal{R}$ e $(a,b),(b,c) \in \mathcal{S}$.
Visto che sono entrambe relazioni transitive:
- $(a,c) \in \mathcal{R}$
- $(a,c) \in \mathcal{S}$
Quindi per definizione di Intersezione, $(a,c) \in \mathcal{R} \cap \mathcal{S}$.

Possiamo quindi confermare che l'Intersezione tra due relazioni transitive ne preserva la transitività.

Verifichiamo ora che lo stesso accada con l'operatore di Unione.

Supponiamo di avere due relazioni transitive: $\mathcal{R}$ = essere più basso di, $\mathcal{B}$ = essere antenato di.

Quindi l'unione $\mathcal{R} \cup \mathcal{B}$ sarà formata dalle coppie in cui o $x$ è antenato di $y$ o $x$ è più basso di $y$.

Pietro è antenato di Valerio, quindi troviamo la coppia (Pietro, Valerio) nell'Unione tra le due Relazioni.
Valerio è più basso di Giuliana, quindi troviamo la coppia (Valerio, Giuliana) nell'Unione tra le due Relazioni.
Pietro non è però più basso di Giuliana ne Giuliana è suo antenato. Quindi sicuramente non troveremo la coppia (Pietro, Giuliana) nell'Unione tra le due Relazioni.
Secondo la Transitività però, se $x$ è più basso di $y$ (Giuliana è più basso di Pietro), allora $x$ è sicuramente più basso di $z$ (Giuliana è più bassa di Valerio).

Possiamo concludere quindi che l'Unione non preserva la Transitività di una Relazione.

Chiusura Transitiva¶

Definizione ― Chiusura Transitiva

La Chiusura Transitiva di una Relazione $\mathcal{R}$ su un insieme $A$ è la relazione più piccola che contiene $\mathcal{R}$ e che è transitiva.

Esempio

\[ \begin{array}{c} A = \{1,2,3\} \\ \mathcal{R} = \{(1,2),(2,3)\} \\ \mathcal{R}^{+} = \{(1,2),(2,3),(1,3)\} \end{array} \]

P-Maggiorabile¶

Definizione ― P-Maggiorabile

Quando esiste un insieme $B$ tale che $P(B)$ e $A \subseteq B$, diciamo che $A$ è P-Maggiorabile.

In altre parole, $A$ è P-Maggiorabile quando rispetta le prime due proprietà della Chiusura.