Skip to content

Modulo 14

Albero delle Proposizioni

Definizione ― Albero delle Proposizioni

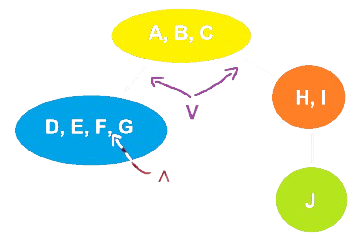
Un Albero delle Proposizioni (o Tableu Proposizionali) è una certa struttura ad albero nella quale ogni nodo può avere zero figli, un figlio, oppure due figli.

  • I nodi sono insiemi di proposizioni.
  • Le proposizioni di ciascun nodo si intendono in congiunzione.
  • I figli di un nodo si intendono in disgiunzione e dipendono dal padre secondo regole costruttive.

image

Note aggiuntive
  • Nelle foglie compaiono solo proposizioni atomiche (\(P,Q,\dots\)) o negazioni di queste (\(\neg P,\neg Q,\dots\)).
Esempio ― AND e OR

image

image

Esempio ― Verificare la Soddisfacibilità di un Albero
  • Prendiamo in considerazione la formula:
\[ \begin{array}{c} P \mathop{\wedge} (\neg Q \mathop{\vee} \neg P) \end{array} \]
  • Possiamo scomporla in questo modo:
\[ \begin{array}{c} P, \neg Q \mathop{\vee} \neg P \end{array} \]
  • A sua volta si può scomporre:
\[ \begin{array}{c} P, \neg Q \\ P, \neg P \end{array} \]
  • Ovviamente \(P, \neg P\) sappiamo che non sarà mai vero perchè è impossibile che abbiano i stessi valori di verità.
  • Quindi, abbiamo individuato il modello che soddisfa la formula di partenza:
\[ \begin{array}{c} m(P) = T \\ m(Q) = F \end{array} \]
  • In questo caso, diciamo che \(P, \neg Q\) è una foglia verde mentre \(P, \neg P\) non lo è.
  • Visto che la formula ha almeno una foglia verde, possiamo concludere che è soddisfacibile.
  • Prendiamo in considerazione la seguente formula:
\[ \begin{array}{c} P \mathop{\wedge} (\neg Q \mathop{\vee} \neg P) \mathop{\wedge} Q \end{array} \]
  • Che possiamo scomporre in:
\[ \begin{array}{c} P,Q,\neg Q \mathop{\vee} \neg P \end{array} \]
  • Ed infine:
\[ \begin{array}{c} P, Q, \neg Q \\ P, Q, \neg P \end{array} \]
  • Entrambe le foglie sono chiuse visto che contengono una proposizione (\(P\)) e la sua negazione (\(\neg P\)).
  • Possiamo concludere che la formula di partenza è insoddisfacibile perchè non esiste un modello in cui è vero \(P,\neg P\) o \(Q, \neg Q\).

Definizione ― Albero Chiuso

Un Albero si dice chiuso quando tutte le sue foglie sono chiuse (contengono falso oppure una proposizione e la sua negazione).

Esempio

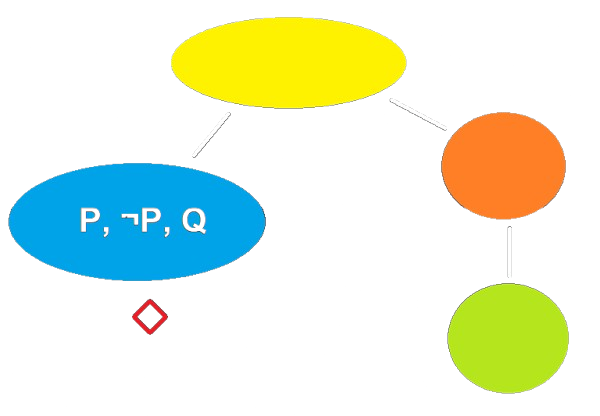
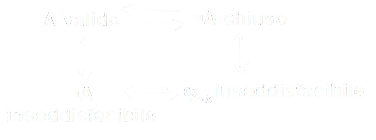
image

Definizione ― Proposizione Valida

Una proposizione \(A\) è valida se e solo se, per ogni \(m\), \(m(A) = T\).
Ovvero, se e solo se per ogni \(m\), \(m(\neg A) = F\).
Ovvero, se e solo se \(\neg A\) è insoddisfacibile.

Regole Costruttive

Definizione ― Regole Costruttive

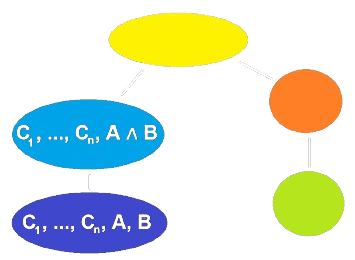
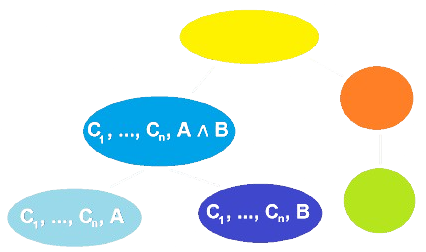
Le seguenti sono regole costruttive che possiamo trovare all'interno di un nodo di un Tableu Proposizionale:

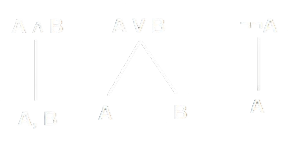
image

Note aggiuntive
  • Le regole costruttive con un solo figlio (\(\mathop{\wedge}\)) sono chiamate regole \(\alpha\).
  • Le regole costruttive con più di un figlio (\(\mathop{\vee}\)) sono chiamate regole \(\beta\).
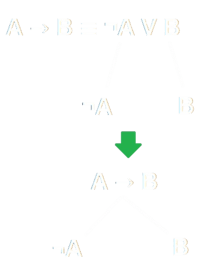
Derivazione di altre Regole Costruttive
  • Dalle tre regole costruttive base possiamo derivarci tutte le altre, per esempio l'implicazione:

image

Proprietà Algebriche
\[ \begin{array}{c} \neg(A \rightarrow B) = A, \neg B \\ \\ \neg (A \rightarrow B) \equiv \neg (\neg A \mathop{\vee} B) \\ \equiv \neg \neg A \mathop{\wedge} \neg B \\ \equiv A \mathop{\wedge} \neg B \\ A, \neg B \end{array} \]

Correttezza e Completezza

Definizione ― Correttezza

La Correttezza si verifica quando un albero \(\neg A\) chiuso implica \(A\) valido.

Definizione ― Completezza

La Completezza si verifica quando un \(A\) valido implica \(\neg A\) chiuso.

Esempio
  • Dato un Tableu di partenza:

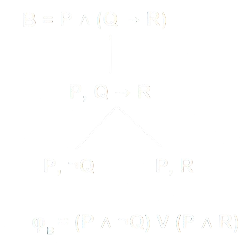
image

  • Analizzando le foglie possiamo ricavare la formula \(\phi_B\), che ha la seguente proprietà:
    • Un qualunque modello \(m\) soddisfa \(B\) (il tableu di partenza) se e solo se soddisfa \(\phi_B\)
    • Inoltre, se \(\phi_B\) è insoddisfacibile, l'albero \(B\) è necessariamente chiuso.
  • Più genericamente quindi, \(A\) è valido se l'albero \(\neg A\) è chiuso. Dimostrazione:

image