Modulo 13

Deduzione Semantica

Definizione ― Deduzione Semantica

Se tutte le proposizioni \(C_1,C_2,\dots,C_n\) e \(A\) sono vere per un certo modello, allora \(B\) deve essere vera nello stesso modello. Inoltre, questo afferma che in tutti i modelli in cui \(C_1,C_2,\dots,C_n\) sono veri, l'implicazione \(A \rightarrow B\) deve essere vera. $$ \begin{array}{c} C_1,C_2,\dots,C_n,A \models B \iff C_1,C_2,\dots,C_n \models A \rightarrow B \end{array} $$

Note aggiuntive

• Se prendiamo un insieme di formule \(C_1,C_2,\dots,C_n\) ed una proposizione \(A\), dire che \(B\) è una conseguenza logica \(\models\) di tutte queste proposizioni è equivalente a dire che l'implicazione \(A \rightarrow B\) è una conseguenza logica delle sole proposizioni \(C_1,C_2,\dots,C_n\).

Esempio

• Prendiamo in considerazione queste proposizioni:

\[ \begin{array}{c} C_1: \text{ "tutti i cani abbaiano"} \\ C_2: \text{ "Bobby è un cane"} \\ A: \text{ " Bobby abbaia"} \\ B: \text{ " Bobby fa rumore"} \end{array} \]

• Vogliamo dimostrare che:

\[ \begin{array}{c} C_1,C_2,\dots,C_n,A \models B \\ \text{ se e solo se } \\ C_1,C_2,\dots,C_n \models A \rightarrow B \end{array} \]

• Parte sinistra della definizione: \(C_1,C_2,A \models B\)
  • Da \(C_1\) \(C_2\), possiamo concludere che \(A\) è vera perchè Bobby è un cane e tutti i cani abbaiano.
  • Con \(A\) vera, anche \(B\) dovrebbe essere vero perchè abbaiare implica fare rumore.
  • Quindi, \(C_1,C_2,A \models B\) è vero per tutti i modelli in cui \(C_1\), \(C_2\) e \(A\) sono veri.
• Parte destra della definizione: \(C_1,C_2 \models A \rightarrow B\)
  • Dobbiamo dimostrare che \(A \rightarrow B\) è vero: "se Bobby abbaia, allora Bobby fa rumore"
  • Dato che \(C_1\) e \(C_2\) sono veri, se Bobby abbaia allora Bobby fa rumore (da definizione di abbaiare).
  • Quindi, \(A \rightarrow B\) è vera nei modelli dove \(C_1\) e \(C_2\) sono veri.

Equivalenza Semantica

Definizione ― Equivalenza Semantica

Due proposizioni \(A\) e \(B\) si dicono semanticamente equivalenti quando, per ogni interpretazione \(m\), \(m(A) = T\) se e solo se \(m(B) = T\).

\[ \begin{array}{c} A \equiv B \end{array} \]

Esempio

• Consideriamo le seguenti proposizioni logiche:

\[ \begin{array}{c} A: \neg p \\ B: p \rightarrow \text{ Falso } \end{array} \]

• Costruiamo la Tabella di Verità per entrambe le proposizioni per tutte le combinazioni di valori di \(p\):

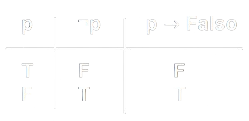
• Possiamo osservare che le colonne per \(\neg p\) e \(p \rightarrow\) Falso hanno gli stessi valori di verità in tutte le interpretazioni.
• Quindi, possiamo concludere che \(\neg p \equiv p \rightarrow\) Falso.

Operatore Logico XOR

Definizione ― XOR

\(A \dot{\vee} B\) è vero quando \(A\) e \(B\) hanno dei valori di verità diversi.

\[ \begin{array}{c} A \dot{\vee} B \end{array} \]

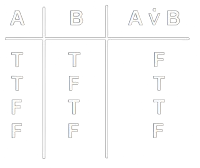
Proprietà Algebriche

\[ \begin{array}{c} A \dot{\vee} B \equiv (A \mathop{\wedge} \neg B) \mathop{\vee} (B \mathop{\wedge} \neg A) \end{array} \]