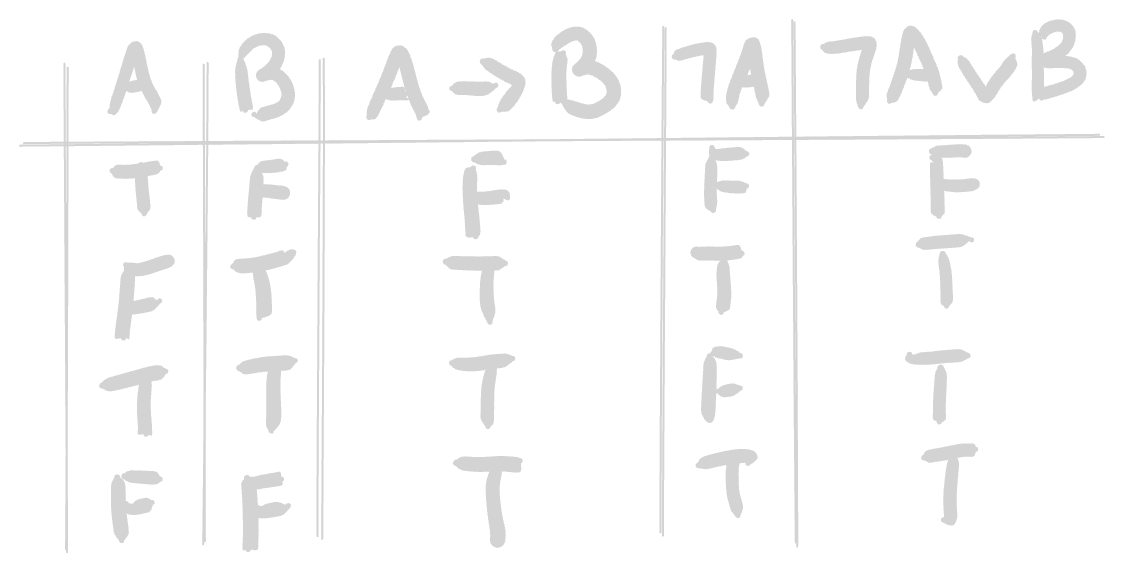Modulo 12
Conseguenza Semantica¶
Definizione ― Conseguenza Semantica
Per ogni modello \(m\), se \(m\) soddisfa \(A_1,A_2,\dots,A_n\), allora \(m\) soddisfa \(B\).
\[
\begin{array}{c}
A_1,A_2,\dots,A_n \models B
\end{array}
\]
Si dice anche che "\(B\) consegue semanticamente da \(A_1,A_2,\dots,A_n\)".
Note aggiuntive
- Quando \(n = 0\), quindi quando non ci sono premesse alla conseguenza semantica, allora per ogni \(m\), \(m\) soddisfa \(B\).
\[
\begin{array}{c}
\models B \\
\\
B \text{ è una Proposizione Valida o Tautologia}
\end{array}
\]
Esempio
- Considerato l'insieme \(\mathbb{N}\) a questo corrisponderà una qualche Algebra di Boole.
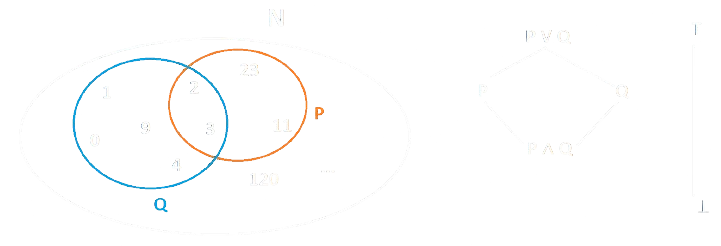
- Ora prendiamo come esempio l'elemento \(9\):
- Possiamo affermare che:
\[
\begin{array}{c}
9 \in Q \\
9 \not\in P \\
\\
m(Q) = T \\
m(P) = F
\end{array}
\]
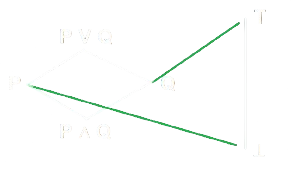
- Una volta individuati \(P\) e \(Q\), possiamo individuare l'interpretazione delle restanti proposizioni (\(P \mathop{\vee} Q\) e \(P \mathop{\wedge} Q\)) attraverso le Tabelle di Verità.
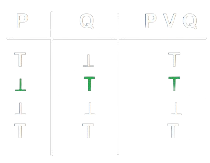 |
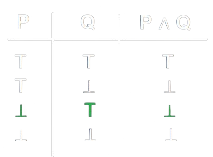 |
|---|---|
\[
\begin{array}{c}
P \mathop{\vee} Q \rightarrow T \\
P \mathop{\wedge} Q \rightarrow F
\end{array}
\]
- Il fatto che \(m(Q)\) sia True, in logica si dice che \(Q\) è vero in \(m\) oppure \(m\) soddisfa \(Q\), usando la seguente notazione:
\[
\begin{array}{c}
\models_m Q
\end{array}
\]
- Quindi: il modello \(m\) assegna True come valore di verità al predicato \(P\).
Implicazione¶
Definizione ― Implicazione
L'Implicazione è un legame tra proposizioni che mette in relazione i valori di verità di due proposizioni matematiche, dette antecedente e conseguente.
Se \(P\) e \(Q\) sono due enunciati, compondendoli col connettivo logico di implicazione materiale si ottiene l'enunciato composto:
\[
\begin{array}{c}
P \rightarrow Q
\end{array}
\]

Esempio
- Dati due enunciati \(P\) = piove e \(Q\) = la strada è bagnata, unendole con il connettivo logico di implicazione materiale si ottiene la proposizione composta:
\[
\begin{array}{c}
P \rightarrow B: \text{ se piove allora la strada è bagnata}
\end{array}
\]
- Se si verifica la causa \(P\) (piove) allora segue l'effetto \(Q\) (la strada è bagnata).
- Se \(P\) e \(Q\) sono proposizioni vere, allora è vero anche l'enunciato \(P \rightarrow Q\), e ciò giustifica la prima riga della Tavola di Verità.
- Se la prima proposizione \(P\) è vera e la seconda \(Q\) è falsa, l'implicazione è falsa, perchè quando si verifica la causa (piove) deve necessariamente verificarsi l'effetto (la strada è bagnata).
- Infine, nel caso in cui la causa \(P\) sia falsa, nulla si può dire sull'effetto \(Q\): infati la strada potrebbe essere bagnata per altri motivi (notte di umidità).
Esempio ― Perchè \(A \implies B = \neg A \mathop{\vee} B\)
- Costruiamo la tabella di verità per entrambe le espressioni \(A \implies B\) e \(\neg A \mathop{\vee} B\), e mostriamo che i valori di verità coincidono per ogni possibile combinazione di \(A\) e \(B\).