Modulo 11
Omomorfismo¶
Definizione ― Omomorfismo
L'omomorfismo è una funzione insiemistica dagli elementi dell'algebra \(\mathbb{A}\) negli elementi dell'algebra \(\mathbb{B}\), che però preserva tutte le operazioni:
\[
\begin{array}{c}
f(a \mathop{\vee} b) = f(a) \mathop{\vee} f(b) \\
f(a \mathop{\wedge} b) = f(a) \mathop{\wedge} f(b) \\
f(\bot) = \bot \\
f(\top) = \top \\
f(\overline{a}) = \overline{f(a)}
\end{array}
\]
Note aggiuntive
- Ci sono alcune funzioni che preservano solo la prima proprietà (operazione di Join), altre solo la seconda (operazione di Meet), in ogni caso per essere un Omomorfismo una funzione deve preservare tutte le operazioni.
- L'Omomorfismo può dividersi in due sottocategorie:
Definizione ― Omomorfismo di Reticoli
Si verifica un Omomorfismo di Reticoli quando sono preservate le prime 3 operazioni (Join, Meet, Top e Bottom).
Definizione ― Omomorfismo di Algebre di Boole
Si verifica un Omomorfismo di Algebre di Boole quando sono preservate tutte le operazioni (Join, Meet, Top e Bottom, Complemento).
Esempio - Non Preservazione di Meet e Join
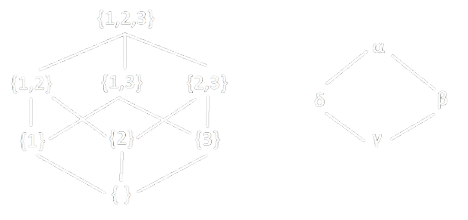
- Dati i Reticoli \(A\) e \(B\) ed una funzione \(f : A \rightarrow B\):
\[
\begin{array}{c}
A = \{\{1,2,3\},\{1,2\},\{1,3\},\{2,3\},\{1\},\{2\},\{3\},\{\}\} \\
B = \{α,β,γ,δ\} \\
\\
f(\{1,2,3\}) = β \\
f(\{1,3\}) = β \\
f(\{2,3\}) = β \\
f(\{3\}) = β \\
f(\{1,2\}) = δ \\
f(\{1\}) = δ \\
f(\{2\}) = δ \\
f(\{\}) = δ
\end{array}
\]
- Dimostriamo le formule, dato \(a = \{1\}\) e \(b = \{3\}\):
\[
\begin{array}{c}
f(a \mathop{\vee} b) = f(a) \mathop{\vee} f(b) \\
f(\{1\} \mathop{\vee} \{3\}) = f(a) \mathop{\vee} f(b) \\
f(sup(\{1\},\{3\})) = f(a) \mathop{\vee} f(b) \\
f(\{1,3\}) = f(a) \mathop{\vee} f(b) \\
β = f(\{1\}) \mathop{\vee} f(\{3\}) \\
β = δ \mathop{\vee} β \\
β = sup(δ,β) \\
β \neq α \\
\\
f(a \mathop{\wedge} b) = f(a) \mathop{\wedge} f(b) \\
f(\{1\} \mathop{\wedge} \{1,3\}) = f(\{1\}) \mathop{\wedge} f(\{3\}) \\
f(inf(\{1\},\{3\})) = f(\{1\}) \mathop{\wedge} f(\{3\}) \\
f(\{\}) = f(\{1\}) \mathop{\wedge} f(\{3\}) \\
δ = δ \mathop{\wedge} β \\
δ = inf(δ,β) \\
δ \neq γ
\end{array}
\]
- Abbiamo dimostrato che questa determinata funzione non è un omomorfismo.
Esempio - Preservazione di Meet e Join
- Dati i Reticoli \(A\) e \(B\) ed una funzione \(f : A \rightarrow B\):
\[
\begin{array}{c}
A = \{\{1,2,3\},\{1,2\},\{1,3\},\{2,3\},\{1\},\{2\},\{3\},\{\}\} \\
B = \{α,β,γ,δ\} \\
\\
f(\{1,2,3\}) = α \\
f(\{1,3\}) = α \\
f(\{2,3\}) = β \\
f(\{3\}) = β \\
f(\{2\}) = γ \\
f(\{\}) = γ \\
f(\{1,2\}) = δ \\
f(\{1\}) = δ
\end{array}
\]
- Dimostriamo le formule, dato \(a = \{1\}\) e \(b = \{3\}\):
\[
\begin{array}{c}
f(a \mathop{\vee} b) = f(a) \mathop{\vee} f(b) \\
f(\{1\} \mathop{\vee} \{3\}) = f(a) \mathop{\vee} f(b) \\
f(sup(\{1\},\{3\})) = f(a) \mathop{\vee} f(b) \\
f(\{1,3\}) = f(a) \mathop{\vee} f(b) \\
α = f(\{1\}) \mathop{\vee} f(\{3\}) \\
α = δ \mathop{\vee} α \\
α = sup(δ,α) \\
α = α \\
\\
f(a \mathop{\wedge} b) = f(a) \mathop{\wedge} f(b) \\
f(\{1\} \mathop{\wedge} \{1,3\}) = f(\{1\}) \mathop{\wedge} f(\{3\}) \\
f(inf(\{1\},\{3\})) = f(\{1\}) \mathop{\wedge} f(\{3\}) \\
f(\{\}) = f(\{1\}) \mathop{\wedge} f(\{3\}) \\
γ = δ \mathop{\wedge} β \\
γ = inf(δ,β) \\
γ = γ
\end{array}
\]
- Abbiamo dimostrato che le prima due proprietà sono preservate (Join e Meet).
- Possiamo anche verificare le restanti proprietà:
- \(f(\bot) = \bot\): l'estremo inferiore dell'algebra \(A\) è mappato nell'estremo inferiore dell'algebra \(B\).
- \(f(\top) = \top\): l'estremo superiore dell'algebra \(A\) è mappato nell'estremo superiore dell'algebra \(B\).
Esempio - Dimostrazione del Complemento
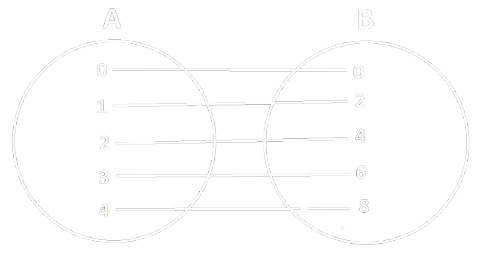
- Dati due insieme \(A\) e \(B\) ed una funzione \(f : A \rightarrow B\):
\[
\begin{array}{c}
A = \{0,1,2,3,4\} \\
B = \{0,2,4,6,8\} \\
f(a) = 2a \\
\\
\text{dimostrazione della formula: } f(\overline{a}) = \overline{f(a)} \\
\text{dato } a = 2 \\
\\
f(\overline{a}) \\
= A - \{2\} = \{0,1,3,4\} \\
f(0) = 0 \\
f(1) = 2 \\
f(3) = 6 \\
f(4) = 8 \\
f(\overline{a}) = \{0,2,6,8\} \\
\\
\overline{f(a)} \\
B - \{f(a)\} \\
= B - \{f(2)\} \\
= B - \{4\} \\
= \overline{f(a)} = \{0,2,6,8\} = f(\overline{a})
\end{array}
\]
Esempio - Introduzione alla Logica Proposizionale
- Consideriamo l'insieme dei numeri naturali \(\mathbb{N}\) ed i due predicati \(P\) e \(Q\):
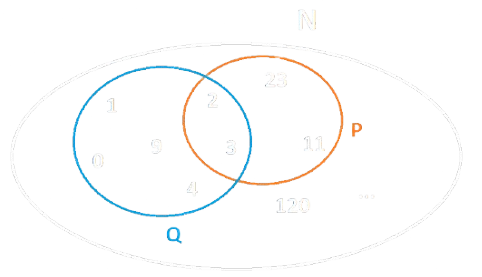
- \(P\) = essere un numero primo
- \(Q\) = essere un numero minore di \(10\)
- Aggiungiamo due Algebre di Boole:
- nella prima Algebra di Boole, ogni elemento rappresenta un sottoinsieme dell'insieme \(\mathbb{N}\)
- la seconda Algebra di Boole è detta Omomorfismo di 2, perchè contiene solo Top e Bottom.
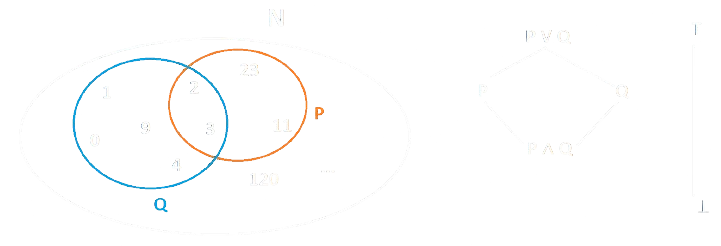
- Preso un qualsiasi elemento \(\mathbb{N}\), mappiamo \(P\) e \(Q\) su \(\top\) / \(\bot\) a seconda se l'elemento di \(\mathbb{N}\) rispetta le proprietà.
Esempio - Omomorfismo Non Violato
- Dato \(a = 2\)
- \(2\) è sia un numero primo (\(P\)) sia è un numero minore di 10 (\(Q\)), quindi entrambi vengono mappati su Top \(\top\).
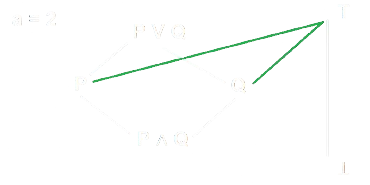
- Gli elementi dell'universo dei sottoinsiemi che corrispondono agli omomorfismi nell'universo delle Algebre di Boole, in realtà corrispondono a delle funzioni che mappano i predicati in Top \(\top\) e Bottom \(\bot\), secondo la condizione descritta nello step precedente:
\[
\begin{array}{c}
P \rightarrow \top \\
Q \rightarrow \bot
\end{array}
\]
Esempio - Omomorfismo Violato
- Esempio con \(a = 9\):
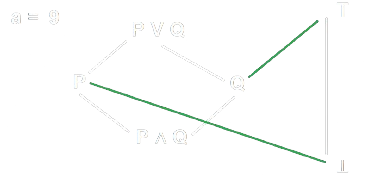
- In questo caso quindi, visto che \(9\) rispetta solo la proprietà \(Q\):
\[
\begin{array}{c}
P \rightarrow \bot \\
Q \rightarrow \top
\end{array}
\]
- Ipotizziamo una funzione \(m\) che oltre a mappare \(P\) e \(Q\), mappa \(P \mathop{\wedge} Q\) su \(\top\).
\[
\begin{array}{c}
P \rightarrow \bot \\
Q \rightarrow \top \\
P \mathop{\wedge} Q \rightarrow ?
\end{array}
\]
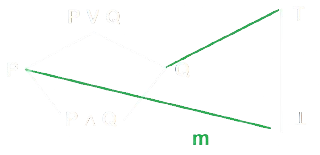
- Dobbiamo quindi trovare una corrispondenza tra l'elemento \(P \mathop{\wedge} Q\) e \(\top\) o \(\bot\).
- Sappiamo che \(\bot\) è composto da \(\bot \mathop{\wedge} \top\).
- Nella particolare funzione \(m\), \(\bot\) corrisponde a \(m(P)\) e \(\top\) corrisponde a \(m(Q)\), quindi possiamo riscrivere la composizione di \(\bot\) in questo modo:
\[
\begin{array}{c}
\bot = m(P) \mathop{\wedge} m(Q)
\end{array}
\]
- Mentre \(\top\) corrisponde al seguente:
\[
\begin{array}{c}
\top = m(P \mathop{\wedge} Q)
\end{array}
\]
- Ricordiamoci che gli omomorfismi devono preservare alcune proprietà, tra cui:
\[
\begin{array}{c}
f(a) \mathop{\wedge} f(b) = f(a \mathop{\wedge} b)
\end{array}
\]
- Nel nostro caso non può essere vero, altrimenti \(\top\) e \(\bot\) sarebbero uguali. Quindi, la funzione \(m\) viola l'omomorfismo.
- Possiamo modificare la funzione \(m\) in questo modo:
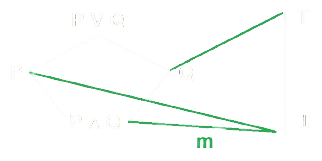
- In questo caso, la funzione \(m\) è un omomorfismo perchè rispetta le tre proprietà:
\[
\begin{array}{c}
P \mathop{\wedge} Q \rightarrow m(P) \mathop{\wedge} m(Q) \\
P \mathop{\vee} Q \rightarrow m(P) \mathop{\vee} m(Q) \\
\neg P \rightarrow \overline{m(P)}
\end{array}
\]
Tavole di Verità¶
Definizione ― Tavole di Verità
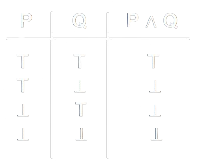
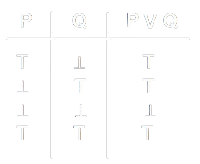
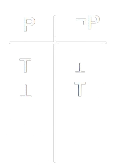
Le Tavole di Verità sono rappresentazioni tabellari che mostrano tutte le possibili combinazioni dei valori di verità (vero o falso, rappresentati rispettivamente da \(T\) e \(F\)) per una o più proposizioni logiche. Sono utilizzate per descrivere il comportamento degli operatori logici, come il join (\(\mathop{\vee}\)) e il meet (\(\mathop{\wedge}\)).
 |
 |
 |
|---|---|---|
Logica Proposizionale¶
Definizione ― Linguaggio della Logica Proposizionale
Combinando le proposizioni elementari (essere un numero primo, essere minore di \(10\), \(\dots\)) con i connettivi logici (and \(\mathop{\wedge}\), or \(\mathop{\vee}\), not \(\neg\)) quello che otteniamo è il Linguaggio della Logica Proposizionale.
Definizione ― Proposizioni
Le Proposizioni possno essere:
- Simboli proposizionali secchi (\(P,Q,\dots\))
- Frasi complesse (proposizioni composte da altre proposizioni)
\[
\begin{array}{c}
A,B, \dots ::= P | Q | \dots | A \mathop{\wedge} B | A \mathop{\vee} B | \neg A | \dots
\end{array}
\]
Esempio
\[
\begin{array}{c}
P \mathop{\wedge} \, (\neg Q \mathop{\vee} R)
\end{array}
\]
- Questa proposizione è composta da altre proposizioni:
- \(P\)
- \(\neg Q\)
- \(R\)
Modello¶
Definizione ― Modello
Un Modello è una Funzione che mappa i simboli proposizionali semplici (\(P,Q,\dots\)) nell'insieme \(\{T,F\}\); mentre per tutte le altre proposizioni (che potrebbero essere frasi complesse) usiamo le tavole di verità per calcolare la loro interpretazione.
Nel mondo della Logica, \(\top\) e \(\bot\) vengono chiamati True e False.
\[
\begin{array}{c}
m : \text{ proposizioni } \rightarrow \{T,F\}
\end{array}
\]
Note aggiuntive
- Non tutte le possibili funzioni che ad ogni proposizione associano \(T,F\) sono modelli legali; per essere modelli devono verificare le tre proprietà and, or, not:
\[
\begin{array}{c}
A \mathop{\wedge} B \rightarrow m(A) \mathop{\wedge} m(B) \\
A \mathop{\vee} B \rightarrow m(A) \mathop{\vee} m(B) \\
\neg A \rightarrow \overline{m(B)}
\end{array}
\]