Modulo 10

Reticoli Distributivi

Definizione ― Reticolo Distributivo

Un Reticolo Distributivo è un reticolo dove è verificata la proprietà distributiva.

\[ \begin{array}{c} a \mathop{\wedge} (b \mathop{\vee} c) = (a \mathop{\wedge} b) \mathop{\vee} (a \mathop{\wedge} c) \\ \\ a \mathop{\vee} (b \mathop{\wedge} c) = (a \mathop{\vee} b) \mathop{\wedge} (a \mathop{\vee} c) \end{array} \]

Esempio ― Reticolo Distributivo

• Partendo dal Reticolo dell'esempio precedente, verifichiamo se è distributivo:

\[ \begin{array}{c} A = \{1,2,3,4,6,12\} \\ \mathcal{R} = \{(a,b) \in A : a \leq b \text{ se e solo se } a \mid b\} \end{array} \]

STEP 4: Verifica della Proprietà Distributiva

\[ \begin{array}{c} a = 2, b = 3, c = 4 \\ \\ 2 \mathop{\wedge} (3 \mathop{\vee} 4) \\ = 2 \mathop{\wedge} mcm(3,4) \\ = 2 \mathop{\wedge} 12 \\ = mcd(2,12) = 2 \\ \\ (2 \mathop{\wedge} 3) \mathop{\vee} (2 \mathop{\wedge} 4) \\ = mcd(2,3) \mathop{\vee} mcd(2,4) \\ = 1 \mathop{\vee} 2 \\ = mcm(1,2) = 2 \\ --- \\ 2 \mathop{\vee} (3 \mathop{\wedge} 4) \\ = 2 \mathop{\vee} mcd(3,4) \\ = 2 \mathop{\vee} 1 \\ = mcm(2,1) = 2 \\ \\ (2 \mathop{\vee} 3) \mathop{\wedge} (2 \mathop{\vee} 4) \\ = mcm(2,3) \mathop{\wedge} mcm(2,4) \\ = 6 \mathop{\wedge} 4 \\ = mcd(6,4) = 2 \\ \\ \dots \end{array} \]

• Conclusione: l'insieme dei numeri divisibili per 12 \(A = \{1,2,3,4,6,12\}\) con la relazione \(\mathcal{R}\) di divisibilità, soddisfa la proprietà distributiva .

Esempio ― Reticolo Non Distributivo

• Dato il seguente reticolo:

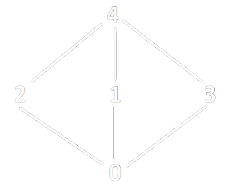
• Usiamo la Proprietà Distributiva per capire se è un reticolo distributivo:

\[ \begin{array}{c} a = 1, b = 2, c = 3 \\ \\ 1 \mathop{\wedge} (2 \mathop{\vee} 3) = (1 \mathop{\wedge} 2) \mathop{\vee} (1 \mathop{\wedge} 3) \\ = 1 \mathop{\wedge} sup(2,3) = inf(1,2) \mathop{\vee} inf(1,3) \\ = 1 \mathop{\wedge} 4 = 0 \mathop{\vee} 0 \\ = inf(1,4) = \sup(0,0) \\ = 1 \neq 0 \end{array} \]

• Conclusione: il Reticolo dato non è un Reticolo Distributivo .

Top e Bottom

Definizione ― Top

In un reticolo \(L\), il Top \(\top\) è l'elemento massimo, ovvero quell'elemento più grande di tutti gli altri.

\[ \begin{array}{c} \forall x \in L, x \leq \top \end{array} \]

Definizione ― Bottom

In un reticolo \(L\), il Bottom \(\bot\) è l'elemento minimo, ovvero quell'elemento più piccolo di tutti gli altri.

\[ \begin{array}{c} \forall x \in L, \bot \leq x \end{array} \]

Esempio

\[ \begin{array}{c} L = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}\} \\ \top = \{1,2,3\} \\ \bot = \emptyset \end{array} \]

• \(\top = \{1,2,3\}\) perchè l'insieme \(\{1,2,3\}\) contiene tutti gli altri sottoinsiemi.
• \(\bot = \emptyset\) perchè è contenuto in tutti gli altri sottoinsiemi.

Applicazione del Teorema su Insiemi Infiniti

• Data un insieme \(A\) infinitamente discendente:

\[ \begin{array}{c} A = \{\dots \leq a_2 \leq a_1 \leq a_0\} \end{array} \]

• Dati qualsiasi due elementi dell'insieme \(A\) avranno sicuramente un \(inf\) ed un \(sup\) (perchè la Relazione \(\leq\) è un Ordinamento Parziale) ma non implica che esista un elemento minimo perchè è una catena infinitamente discendente.

Proprietà Algebriche

\[ \begin{array}{c} \textit{Assiomi di Identità} \\ A \mathop{\vee} \bot = A \\ A \mathop{\wedge} \top = A \\ \\ \forall (a,b,c), \\ \text{ se } a \mathop{\vee} b = a \mathop{\vee} c \\ \text{e } a \mathop{\wedge} b = a \mathop{\wedge} c, \\ \text{allora } b = c \\ \\ \text{in sintesi: se } b \text{ e } c \text{ si comportano allo stesso modo se dati in pasto al meet/join di } a, \\ \text{allora (se siamo in un reticolo distributivo) questo può avvenire solo se } b=c \end{array} \]

Complemento

Definizione ― Complemento

Un elemento \(\overline{a}\) di un Reticolo \(A\) si dice complemento di \(a \in A\) se:

\[ \begin{array}{c} a \mathop{\vee} \overline{a} = \top \\ a \mathop{\wedge} \overline{a} = \bot \end{array} \]

Definizione ― Unicità del Complemento

In un Reticolo Distributivo, se \(a \in A\) ha un complemento, allora non può averne altri.

Non è vero il contrario: esistono Reticoli Non Distributivi a complemento unico ― ma non esistono esempi!

Dimostrazione delle Proprietà Algebriche

• Dato un insieme potenza costituito da:

\[ \begin{array}{c} (2^A, \cup,\cap,-,\{\},A) \end{array} \]

• In cui:
  • \(2^A\) rappresenta l'insieme di tutti i sottoinsiemi di \(A\)
  • \(\cup\) rappresenta il join \(\mathop{\vee}\)
  • \(\cap\) rappresenta il meet \(\mathop{\wedge}\)
  • \(-\) rappresenta l'operazione di complemento
  • \(\{\}\) rappresenta il \(min(A)\) \(\bot\)
  • \(A\) rappresenta il \(max(A)\) \(\top\)

• Possiamo dimostrare che le proprietà algebriche si verificano correttamente:

\[ \begin{array}{c} a \mathop{\vee} \overline{a} = B \cup \overline{B} = A = \top \\ a \mathop{\wedge} \overline{a} = B \cap \overline{B} = \{\} = \bot \end{array} \]

Convoluzione

Definizione ― Convoluzione

Il complemento di un complemento ritorna l'elemento originale. Questa operazione è detta Convoluzione.

\[ \begin{array}{c} \overline{\overline{A}} = A \end{array} \]

Dualità di Stone

Definizione ― Dualità di Stone

Ogni Algebra di Boole (rappresentazione astratta di un reticolo) è isomorfa ad un'algebra di insieme (rappresentazione concreta di un insieme).

Leggi di De Morgan

Definizione ― Leggi di De Morgan

\[ \begin{array}{c} \overline{A \mathop{\vee} B} = \overline{A} \mathop{\wedge} \overline{B} \\ \overline{A \mathop{\wedge} B} = \overline{A} \mathop{\vee} \overline{B} \end{array} \]

Algebra di Boole

Definizione ― Algebra di Boole

L'Algebra di Boole è una struttura algebrica con:

• un insieme
• due elementi speciali: Top \(\top\), Bottom \(\bot\)
• tre operazioni: Join \(\mathop{\vee}\), Meet \(\mathop{\wedge}\), Complemento \(\overline{A}\)

Ogni Algebra di Boole è necessariamente un Reticolo Distributivo.